Voxel Graph Operators; Topological Voxelization, Graph Generation, and Derivation of Discrete Differential Operators from Voxel Complexes

Abstract:

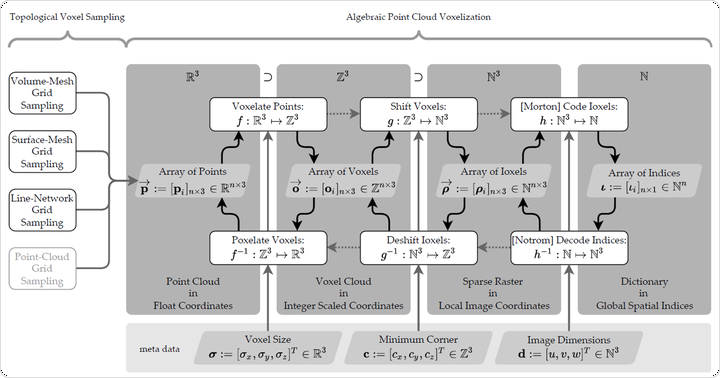
In this paper, we present a novel workflow consisting of algebraic algorithms and data structures for fast and topologically accurate conversion of vector data models such as Boundary Representations into voxels (topological voxelization); spatially indexing them; constructing connectivity graphs from voxels; and constructing a coherent set of multivariate differential and integral operators from these graphs. Topological Voxelization is revisited and presented in the paper as a reversible mapping of geometric models from ${\mathbb{R}}^3$ to ${\mathbb{Z}}^3$ to ${\mathbb{N}}^3$ and eventually to an index space created by Morton Codes in $\mathbb{N}$ while ensuring the topological validity of the voxel models; namely their topological thinness and their geometrical consistency. In addition, we present algorithms for constructing graphs and hyper-graph connectivity models on voxel data for graph traversal and field interpolations and utilize them algebraically in elegantly discretizing differential and integral operators for geometric, graphical, or spatial analyses and digital simulations. The multi-variate differential and integral operators presented in this paper can be used particularly in the formulation of Partial Differential Equations for physics simulations.